What is manifold fitting?

This is a quick introduction of manifold fitting. A PDF version is also available. More details can be found in:

• Fefferman, C., Ivanov, S., Kurylev, Y., Lassas, M., & Narayanan, H. (2018, July). Fitting a putative manifold to noisy data. In Conference On Learning Theory (pp. 688-720). PMLR.
• Yao, Z., & Xia, Y. (2019). Manifold fitting under unbounded noise. arXiv preprint arXiv:1909.10228.
• Yao, Z., Su, J., Li, B., & Yau, S. T. (2023). Manifold fitting. arXiv preprint arXiv:2304.07680.

Overview

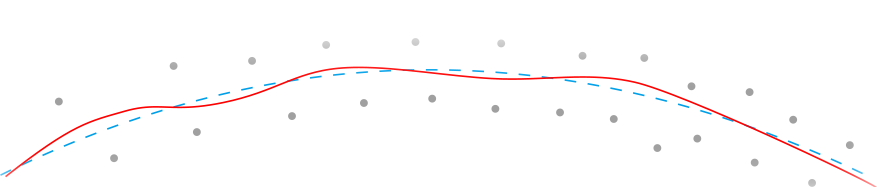
In recent years, there has been a growing interest in non-Euclidean statistical analysis, particularly in the pursuit of recovering a low-dimensional structure, referred to as a manifold, that underlies high-dimensional data. The successful recovery of this manifold is contingent on certain noise concentration conditions. Previous methods tackle this challenge by approximating the manifold based on tangent space estimations at each data sample. While these methods offer theoretical convergence guarantees, they assume either noise-free data or noise with bounded characteristics. In practical scenarios where unbounded noise is common, the tangent space estimations at noisy samples become inherently imprecise, potentially introducing inaccuracies when fitting the manifold.

In response to this challenge, our research project introduces a novel approach. Instead of estimating tangent spaces at the original data samples, we directly estimate these spaces at projected points on the underlying manifold. This strategic shift aims to mitigate errors caused by unbounded noise, resulting in more accurate manifold fitting.

Our research, encompassing our 2019 paper (yx) and subsequent work in 2023 (ysl), centers on non-Euclidean statistical analysis, specifically the recovery of low-dimensional manifolds from high-dimensional data. Unlike existing methods relying on tangent space estimations at data samples, we directly estimate these spaces at manifold-projected points, enhancing accuracy and addressing unbounded noise. Our initial paper (yx) introduced a practical algorithm for manifold fitting, and our 2023 work (ysl) refines the algorithm and establishes superior error bounds. These contributions significantly advance non-Euclidean statistical analysis.

Model Setting

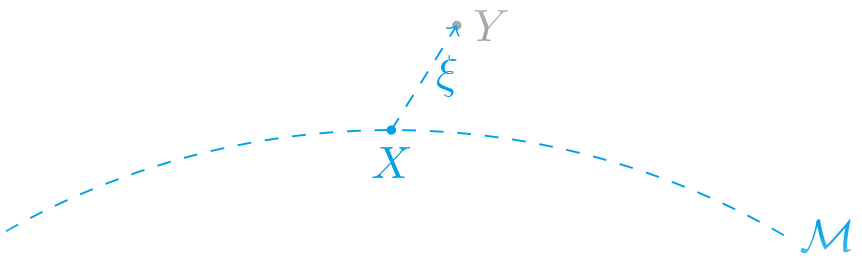
Let \(\mathcal{M}\) be a \(d\)-dimensional smooth latent manifold embedded in the ambient space \(\mathbb{R}^D\). In this problem, we focus on a random vector \(Y \in \mathbb{R}^D\) that can be expressed as

\[Y = X + \xi,\]

where \(X \in \mathbb{R}^D\) is an unobserved random vector following a distribution \(\omega\) supported on the latent manifold \(\mathcal{M}\), and \(\xi \sim \phi_\sigma\) represents the ambient-space observation noise, independent of \(X\), with a standard deviation \(\sigma\). The distribution of \(Y\) can be viewed as the convolution of \(\omega\) and \(\phi_\sigma\), whose density at point \(y\) can be expressed as

\[\nu(y) = \int_\mathcal{M} \phi_\sigma(y-x)\omega(x)d x.\]

Assume \(\mathcal{Y} = \{y_i\}_{i=1}^N \subset \mathbb{R}^D\) is the collection of observed data points, also in the form of

\[y_i = x_i + \xi_i, \quad \text{ for } i = 1,\cdots,N,\]

with \((y_i, x_i,\xi_i)\) being \(N\) independent and identical realizations of \((Y,X,\xi)\). Based on \(\mathcal{Y}\), we construct an estimator \(\widehat{\mathcal{M}}\) for \(\mathcal{M}\) and provide theoretical justification for it under the following main assumptions:

• The latent manifold \(\mathcal{M}\) is a compact and twice-differentiable \(d\)-dimensional sub-manifold, embedded in the ambient space \(\mathbb{R}^D\). Its volume with respect to the \(d\)-dimensional Hausdorff measure is upper bounded by \(V\), and its reach¹ is lower bounded by a fixed constant \(\tau\).

• The distribution \(\omega\) is a smooth distribution, with respect to the \(d\)-dimensional Hausdorff measure, on \(\mathcal{M}\).

• The noise distribution \(\phi_\sigma\) is a Gaussian distribution supported on \(\mathbb{R}^D\) with density function

\[\phi_\sigma (\xi)= (\frac{1}{2\pi \sigma^2})^{\frac{D}{2}}\exp{(-\frac{\|\xi\|_2^2}{2\sigma^2})}.\]

• The intrinsic dimension \(d\) and noise standard deviation \(\sigma\) are known.

The manifold estimator \(\widehat{\mathcal{M}}\) is suppose to be

• \(d\)-dimensional smooth manifold with lower bounded reach;
• close to \(\mathcal{M}\).

---